轻松掌握：十进制数转为二进制与十六进制的技巧

十进制转换成二进制和十六进制的奥秘

在计算机科学和数字系统中，不同的数制扮演着至关重要的角色。其中，十进制、二进制和十六进制是最常用的数制。十进制是我们日常生活中最熟悉的数制，即逢十进一。而二进制则是计算机内部存储和处理数据的基石，它基于两个基本符号0和1。十六进制则是一种方便于人类阅读和书写的数制，特别是在处理二进制数据时，它作为一种中间表示形式非常有用。那么，十进制是如何转换成二进制和十六进制的呢？让我们一探究竟。

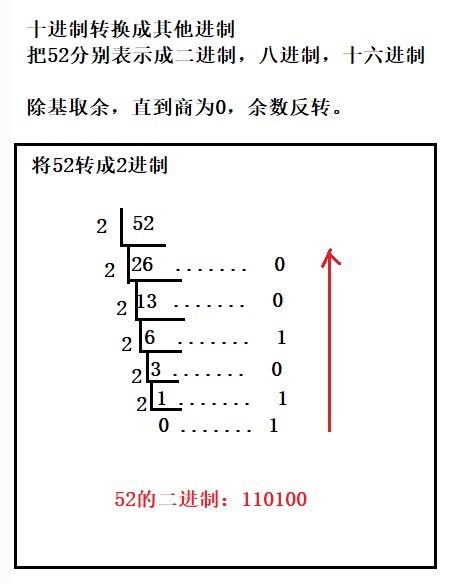
首先，我们来看看十进制如何转换成二进制。这个过程涉及到的是“除2取余法”。简单来说，就是将十进制数不断除以2，记录下每次除法的余数，然后将这些余数从最后一位开始往前排列，得到的数就是该十进制数的二进制表示。

举个例子，假设我们要将十进制数23转换成二进制。首先，23除以2，商为11，余数为1；然后，11再除以2，商为5，余数为1；接着，5除以2，商为2，余数为1；最后，2除以2，商为1，余数为0。将这些余数从最后一位开始排列，我们得到的就是23的二进制表示：10111。

需要注意的是，在转换过程中，如果得到的商为0，那么转换过程就结束了。另外，二进制数的最低位（也就是最右边的位）代表2的0次方，即1；然后依次向左，每一位代表的值分别是2的1次方、2的2次方、2的3次方……以此类推。

那么，十进制数又是如何转换成十六进制的呢？这个过程与转换成二进制类似，但是基数变成了16。在十六进制中，我们用0到9表示10以内的数，而用A到F表示10到15。因此，转换过程中的“取余”步骤得到的余数范围是在0到15之间。

同样地，我们采用“除16取余法”来进行转换。将十进制数不断除以16，记录下每次除法的余数，然后将这些余数从最后一位开始往前排列，得到的数就是该十进制数的十六进制表示。如果余数在10到15之间，则用A到F来表示。

以十进制数233为例，我们将其转换成十六进制。首先，233除以16，商为14，余数为9；然后，14再除以16，由于14小于16，所以商为0，余数就是14，在十六进制中用E表示。因此，233的十六进制表示为E9。

在十六进制中，最低位代表16的0次方，即1；然后依次向左，每一位代表的值分别是16的1次方、16的2次方、16的3次方……以此类推。

了解了十进制转换成二进制和十六进制的方法后，我们可能会好奇，为什么计算机要使用二进制而不是十进制呢？这主要是因为二进制具有一些独特的优点，使得它成为计算机内部存储和处理数据的最佳选择。

首先，二进制只有两个基本符号0和1，这使得它在计算机内部的实现非常简单。计算机内部的电路可以很容易地表示这两种状态，从而实现了数据的存储和处理。

其次，二进制运算规则简单，易于实现。与十进制相比，二进制在加减乘除等运算过程中所需的规则要少得多，这大大降低了计算机设计的复杂性。

此外，二进制还具有抗干扰能力强、可靠性高等优点。由于二进制中只有0和1两种状态，所以在数据传输和存储过程中，即使受到一定程度的干扰，也能很容易地恢复出原始数据。

而十六进制作为二进制的一种中间表示形式，也具有一些独特的优点。首先，十六进制数在书写和阅读上比二进制数要方便得多。由于每一位十六进制数可以表示4位二进制数（因为16等于2的四次方），所以在表示相同的数据时，十六进制数比二进制数要简短得多。

其次，十六进制数与二进制数之间的转换非常方便。由于十六进制数的每一位都可以直接对应到二进制数的4位，所以在转换过程中不需要进行复杂的计算。

综上所述，十进制、二进制和十六进制各有其独特的优点和适用范围。在计算机科学和数字系统中，它们相互补充、相互支持，共同构成了数字世界的基石。通过了解它们之间的转换方法，我们可以更好地理解和应用这些数制，从而在计算机科学领域取得更大的进步。

对于那些对“十进制怎样转换成二进制和十六进制”感兴趣的朋友来说，掌握这些方法不仅可以帮助我们更好地理解计算机科学的基础知识，还可以在实际应用中发挥重要作用。无论是在编程、数据分析还是其他计算机科学领域，这些数制转换的知识都是不可或缺的。因此，让我们一起努力学习并应用这些知识吧！