弧度应该如何计算？

在数学和物理中，弧度是角度的一种度量方式，它为我们提供了一种更直观、更自然的描述圆周运动和周期性现象的方法。与度相比，弧度在许多数学公式和物理定律中表现得更加简洁和优雅。那么，弧度应该怎么算呢？下面，我们将详细探讨弧度的定义、计算方法及其在各个领域的应用。

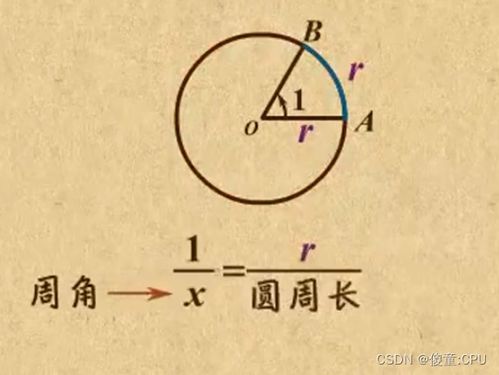
首先，我们需要明确弧度的基本概念。弧度是一种角度的度量单位，它表示的是圆上一段弧的长度与圆的半径的比值。具体来说，如果一个圆的半径为r，圆上的一段弧的长度为l，那么这段弧所对应的圆心角的大小（以弧度为单位）就是l/r。从这个定义可以看出，弧度的大小与圆的半径无关，只与弧长有关。

接下来，我们来看如何计算弧度。假设我们有一个圆，其半径为r，圆上有一段弧，其对应的圆心角为θ（以弧度为单位），那么这段弧的长度l就可以通过公式l=r×θ来计算。反之，如果我们知道弧长l和半径r，那么就可以通过公式θ=l/r来计算圆心角θ的大小（以弧度为单位）。

在实际应用中，我们经常需要将角度从度转换为弧度，或者从弧度转换为度。这可以通过特定的换算公式来实现。具体来说，180度等于π弧度，所以度（D）和弧度（R）之间的换算关系可以通过以下公式来表示：R=D×π/180，D=R×180/π。例如，如果我们想要将45度转换为弧度，那么就可以使用公式R=45×π/180，计算得出R=π/4。同样地，如果我们想要将π/3弧度转换为度，那么就可以使用公式D=π/3×180/π，计算得出D=60度。

在计算弧度时，我们还需要注意一些特殊情况。例如，当圆心角为0度时，其对应的弧度为0；当圆心角为180度时，其对应的弧度为π；当圆心角为360度时，其对应的弧度为2π。这些特殊情况在计算弧度和处理圆周运动时非常重要。

除了上述的基本概念和计算方法外，弧度在许多数学公式和物理定律中都有着广泛的应用。例如，在三角函数中，弧度是函数定义域的基本单位。正弦、余弦、正切等三角函数都是以弧度为单位来定义的。在物理学中，弧度也经常被用来描述圆周运动和周期性现象。例如，在简谐振动中，物体的位移、速度和加速度等物理量都可以表示为时间和角频率的函数，而角频率的单位就是弧度每秒。

此外，弧度在几何学和微积分学中也有着重要的应用。在几何学中，弧度可以帮助我们更好地理解圆的性质和圆的切线等问题。在微积分学中，弧度则是导数和积分等概念的基础。例如，在求圆的周长和面积时，我们需要用到弧度的概念。圆的周长公式C=2πr和面积公式S=πr²都是以弧度为基础推导出来的。

在计算弧度时，我们还可以借助一些辅助工具来提高计算的准确性和效率。例如，我们可以使用计算器来计算弧度和度之间的换算关系，以及使用三角函数表来查找特定角度下的三角函数值。此外，随着计算机技术的发展，我们还可以使用各种数学软件和编程语言来进行更加复杂的弧度计算和数据处理。

需要注意的是，虽然弧度和度都是角度的度量单位，但在某些情况下，它们的使用是有所区别的。例如，在计算三角函数值时，我们通常使用弧度作为角度的单位；而在描述物体在平面上的旋转方向时，我们则通常使用度作为角度的单位。因此，在使用弧度和度时，我们需要根据具体的上下文和应用场景来选择合适的单位。

综上所述，弧度是一种重要的角度度量单位，它在数学、物理和工程学等领域都有着广泛的应用。通过掌握弧度的基本概念和计算方法，我们可以更好地理解圆的性质和圆周运动规律，以及解决各种与角度相关的问题。同时，我们还需要注意弧度和度之间的换算关系以及它们在不同领域中的应用差异，以便在实际应用中能够正确地选择和使用合适的单位。

在计算弧度时，我们还需要注意一些细节问题。例如，在计算弧长时，我们需要确保所给的圆心角是对应弧所对的圆心角；在计算三角函数值时，我们需要将角度转换为弧度后再进行计算；在描述物体的旋转方向时，我们需要注意区分顺时针旋转和逆时针旋转所对应的角度正负号等。只有正确地处理这些细节问题，我们才能确保计算结果的准确性和可靠性。